Lab 2

SIMPLIFICACIÓN E IMPLEMENTACIÓN FÍSICA DE CIRCUITOS LÓGICOS

      I.     CAPACIDAD TERMINAL

·        Reconocer las áreas de aplicación de la Electrónica Digital.

·        Identificar las características de los dispositivos digitales más utilizados.

·         Diseñar sistemas combinacionales y secuenciales.

      I.     COMPETENCIA ESPECIFICA DE LA SESION

·         Simplificar funciones lógicas utilizando Mapas de Karnaugh.

·         Implementar y probar funciones lógicas.

·         Conocer las principales Familias lógicas: TTL y CMOS

      I.        CONTENIDOS A TRATAR

·         Uso de las técnicas de simplificación en la reducción de funciones lógicas.

OBJETIVOS

-Describir la operación de las tablas de la verdad para las compuertas AND,NAND, OR, NOR y construirlas.

-Escribir las combinaciones de compuertas lógicas en un circuito simple y obtener compuertas combinadas.

-Analizar los resultados experimentales.

 -Formar una capacidad de análisis critica, para interpretar de una manera óptima los resultados obtenidos, de una forma lógica como analítica

.

TEORÍA DE SIMPLIFICACIÓN DE FUNCIONES MEDIANTE MAPAS DE KARNAUGH.

Los Mapas de Karnaugh son una herramienta muy utilizada para la simplificación de circuitos lógicos. Cuando se tiene una función lógica con su tabla de verdad y se desea implementar esa función de la manera más económica posible se utiliza este método.

Ejemplo: Se tiene la siguiente tabla de verdad para tres variables. Se desarrolla la función lógica basada en ella. (primera forma canónica). Ver que en la fórmula se incluyen solamente las variables (A, B, C) cuando F cuando es igual a “1”. Si A en la tabla de verdad es “0” se pone A, si B = “1” se pone B, Si C = “0” se pone C, etc.

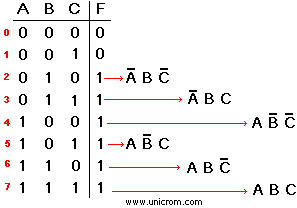
F = A B C + A B C + A B C + A B C + A B C + A B C

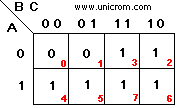
Una vez obtenida la función lógica, se implementa el mapa de Karnaugh. Este tiene 8 casillas que corresponden a 2n, donde n = 3 (número de variables (A, B, C)). Ver el diagrama arriba a la derecha. La primera fila corresponde a A = 0 La segunda fila corresponde a A = 1 La primera columna corresponde a BC = 00 (B=0 y C=0) La segunda columna corresponde a BC = 01 (B=0 y C=1) La tercera columna corresponde a BC = 11 (B=1 y C=1) La cuarta columna corresponde a BC = 10 (B=1 y C=0)

En el mapa de Karnaugh se han puesto “1” en las casillas que corresponden a los valores de F = “1” en la tabla de verdad. Tomar en cuenta la numeración de las filas de la tabla de verdad y la numeración de las casillas en el mapa de Karnaugh.

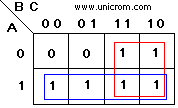
Para proceder con la simplificación, se crean grupos de “1”s que tengan 1, 2, 4, 8, 16, etc. (sólo potencias de 2). Los “1”s deben estar adyacentes (no en diagonal) y mientras más “1”s tenga el grupo, mejor. La función mejor simplificada es aquella que tiene el menor número de grupos con el mayor número de “1”s en cada grupo

Se ve del gráfico que hay dos grupos cada uno de cuatro “1”s, (se permite compartir casillas entre los grupos). La nueva expresión de la función boolena simplificada se deduce del mapa de Karnaugh.

• Para el primer grupo (rojo): la simplificación da B (los “1”s de la tercera y cuarta columna corresponden a B sin negar)
• Para el segundo grupo (azul): la simplificación da A (los “1”s están en la fila inferior que corresponde a A sin negar)

Entonces el resultado es F = B + A  ó   F = A + B

Ejemplo: Una tabla de verdad como la de la derecha da la siguiente función booleana: F = A B C + A B C + A B C + A B C

Se ve claramente que la función es un reflejo del contenido de la tabla de verdad cuando F = “1”, Con esta ecuación se crea el mapa de Karnaugh y se escogen los grupos. Se lograron hacer 3 grupos de dos “1”s cada uno. Se puede ver que no es posible hacer grupos de 3, porque 3 no es potencia de 2. Se observa que hay una casilla que es compartida por los tres grupos.

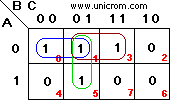
La función simplificada es: F = A B+ A C + B C. Grupo en azul: A B, grupo marrón: A C, grupo verde:B C

implementación física del circuito lógico

                              

ACTIVIDAD

   RESOLVER el problema para automatizar el RIEGO de una planta.

    Se desea hacer un circuito de riego automático como el mostrado en la figura. El circuito deberá accionar la bomba en las siguientes condiciones:

·         El circuito accionará la bomba solamente cuando la tierra esté seca, pero antes debe comprobar  las siguientes condiciones:

·         Para evitar que la bomba se estropee por funcionar en vacío, nunca se accionará la bomba cuando el depósito de agua esté vacío.

·         Si hay restricciones en el riego (época de verano), sólo se podrá regar de noche. En el resto del año (si no hay restricciones) se podrá regar de día y de noche (si la tierra está seca).

Para la implementación del circuito se dispone de las siguientes entradas:

S: Señal que indica si la tierra está seca.

            Tierra seca: S=1 ; Tierra húmeda: S=0

R: Señal que indica si hay restricciones en el riego (es verano):

            Hay restricciones: R=1 No hay restricciones: R=0

D: Señal que indica si es de día o de noche:

            Día: D=1 ; Noche: D=0

V: Señal que indica si el depósito de agua está vacío:

            Vacío: V=1 ; Hay agua: V=0

Y la salida B, que accionará la bomba para regar: Bomba funcionando: B=1 ; Bomba apagada B=0

VIDEO DEMOSTRATIVO DE LA RESOLUCIÓN DE LA ACTIVIDAD 

       

VIDEO DEMOSTRATIVO DE LA  IMPLEMENTACION FISICA 

       

OBSERVACIONES

-Se observo problemas en el armado pero se pudo concluir con éxito  
- se observo  la  facultad de poder analizar las  compuertas  tratadas  según su funcionalidad  en la comprensión y facultad al poder armarlo   

CONCLUSIONES

-Con este laboratorio pudimos observar que a partir de compuertas sencillas podemos obtener otras compuertas un poco más complejas, esto es de sumaimportancia en el caso que tengamos que armar circuitos y ciertos tipos de las mismas no estén en el mercado.

-Aplicamos las leyes de Morgan en este informe, que en pocas palabras no es más que una ley para reducir la expresión del circuito (la salida) a una expresión más corta y que cumpla con la tabla de la verdad del mismo

-Por otra parte aprendimos a utilizar el ISIS PROTEUS, que es un programa parasimular circuitos digitales y así pudimos comprobar tanto los circuitos simuladoscomo los armados en protoboard.

-Con ayuda de los apuntes de las clases pudimos resolver las ecuaciones de las diferentes compuertas pudiendo así escribir una ecuación de salida, y con la ayuda de las Leyes de Morgan antes mencionadas reducimos esa expresión

INTEGRANTES :

MAMANI DE LA CRUZ GUSTAVO

MAMANI BERNAL ARTURO